
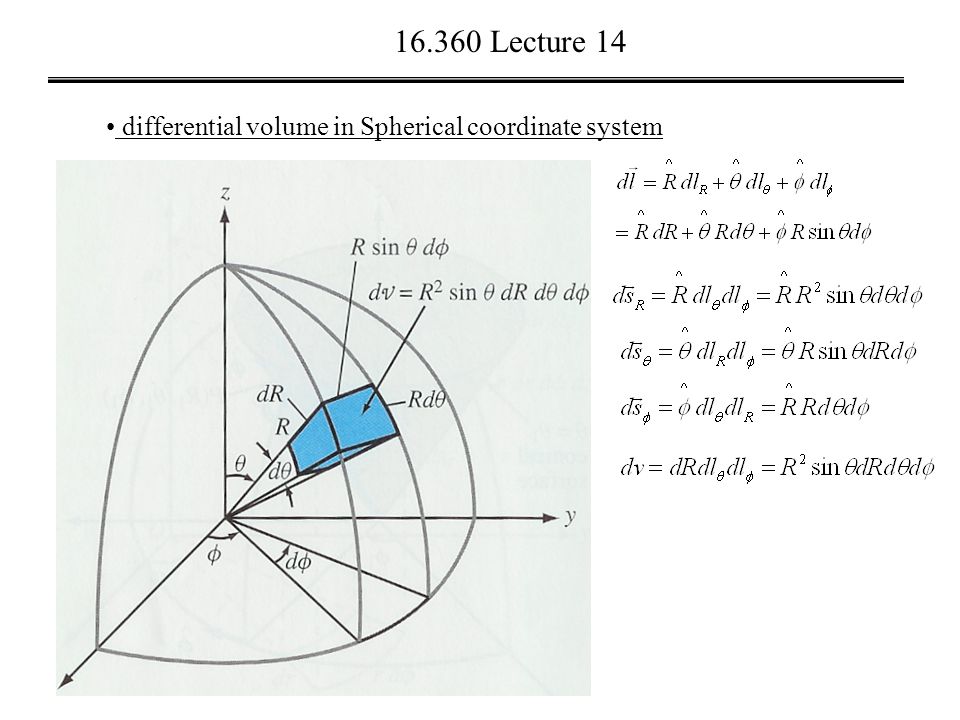
1.3 RELATION BETWEEN CARTESIAN AND CYLINDRICAL COORDINATE SYSTEM Spherical coordinates make it simple to describe a sphere, just as cylindrical coordinates make it easy to describe a cylinder. In this case, the triple describes one distance and two angles. In the spherical coordinate system, we again use an ordered triple to describe the location of a point in space.

In the Cartesian coordinate system, the location of a point in space is described using an ordered triple in which each coordinate represents a distance. The equations can often be expressed in more simple terms using cylindrical coordinates. These systems have complicated modeling equations in the Cartesian coordinate system, which make them difficult to describe and analyze. Physicists studying electrical charges and the capacitors used to store these charges have discovered that these systems sometimes have a cylindrical symmetry. The use of cylindrical coordinates is common in fields such as physics. In this case, the z -coordinates are the same in both rectangular and cylindrical coordinates. Use the second set of equations from Note to translate from rectangular to cylindrical coordinates. This is exactly the same process that we followed in Introduction to Parametric Equations and Polar Coordinates to convert from polar coordinates to two-dimensional rectangular coordinates. If this process seems familiar, it is with good reason.
#RECTANGULAR TO CYLINDRICAL COORDINATE CALCULATOR LICENSE#
Cisco 9500 license activationĬonversion from cylindrical to rectangular coordinates requires a simple application of the equations listed in Note. In other words, these surfaces are vertical circular cylinders.
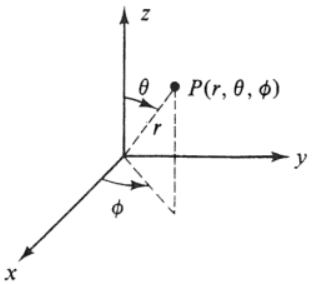
Notice that these equations are derived from properties of right triangles. In this way, cylindrical coordinates provide a natural extension of polar coordinates to three dimensions. Starting with polar coordinates, we can follow this same process to create a new three-dimensional coordinate system, called the cylindrical coordinate system. When we expanded the traditional Cartesian coordinate system from two dimensions to three, we simply added a new axis to model the third dimension. Similarly, spherical coordinates are useful for dealing with problems involving spheres, such as finding the volume of domed structures.

As the name suggests, cylindrical coordinates are useful for dealing with problems involving cylinders, such as calculating the volume of a round water tank or the amount of oil flowing through a pipe. In this section, we look at two different ways of describing the location of points in space, both of them based on extensions of polar coordinates. This is a familiar problem recall that in two dimensions, polar coordinates often provide a useful alternative system for describing the location of a point in the plane, particularly in cases involving circles. Some surfaces, however, can be difficult to model with equations based on the Cartesian system. Question feed.The Cartesian coordinate system provides a straightforward way to describe the location of points in space. Responding to the Lavender Letter and commitments moving forward. Narasimham Narasimham Or am I getting something wrong? Sign up or log in Sign up using Google. Carl Carl 3 3 silver badges 11 11 bronze badges. Home Questions Tags Users Unanswered.Ĭonvert function from cartesian coordinates to cylindrical and spherical Ask Question. The best answers are voted up and rise to the top. Is there some method to convert an entire expression into a different coordinate system? That is, how do I convert my expression from cartesian coordinates to cylindrical and spherical so that the expression for the electric field looks like this for the cylindrical. This point charge is placed in the origin of an orthogonal coordinate system. Mathematics Stack Exchange is a question and answer site for people studying math at any level and professionals in related fields. By using our site, you acknowledge that you have read and understand our Cookie PolicyPrivacy Policyand our Terms of Service.


 0 kommentar(er)
0 kommentar(er)
